Term - Géométrie Analytique: Calcul Vectoriel

[ThePunisher]

Calcul Vectoriel

1.1 Vecteurs liés et vecteurs libres.

1) Vecteurs liés.

Définition 1: Un vecteur lié (ou bipoint) est un couple ordonné de point (A,B). On le représente par un segment de droite orienté et on le note (A,B).

On y associe:
-Son origine A.
-Son extrémité B.
-Sa direction (ensemble des droites parallèles à (AB) )
-Son sens.
-Sa norme.

Definition 2:
Deux vecteurs liés sont égaux si et seulement si ils ont même origine et même extrémité.

(A,B)=(C,D)<=> A=C et B=D

Remarque:
Si A=/=B, alors (A,B) et (C,D) sont différents, ils ont même direction et même norme mais ils sont de sens opposés. Ces vecteurs sont donc dits opposés.

Definition 3:
Deux vecteurs liés (A,B) et (C,D) sont dits équipollents s'ils ont même direction, même sens et même norme. Ce terme est réservé au vecteurs liés.
On écrit alors (A,B) ~ (C,D).

Caractérisation géométrique:
-(A,B) ~ (C,D) <=> ACDB est un parallèlogramme. (éventuellement dégénéré => plat)
-(A,B) ~ (C,D) <=> AD et BC ont même point milieu.

Définition 4:
Soit (A,B) un vecteur lié. On appelle classe d'équipollence de (A,B) l'ensemble des vecteurs équipolents à (A,B).
On la note :

={(m,N)|(M,N)~(A,B)}
Cela signifie que est égal à tout vecteur lié (M,N) tel que (M,N) et (A,B) soient équipollents. On conclus donc que: (A,B),(M,N) sont les représentants de la classe

Propriétés:
-(A,B) ~ (C,D) <=> =
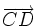
-Tout vecteur lié appartient à une et une seule classe.
-Deux classes sont distinctes ou confondues.




2) Vecteurs libres

Definition: Un vecteur libre est une classe d'équipollence de vecteurs liés.

Un vecteur libre est donc défini par:

--> Sa direction
--> Son sens
--> Sa norme (longueur) notée ||AB|| (par manque de caractères, considèrez toutes les lettres ou couple de lettres comme des vecteurs, avec donc une flèche au dessus)

On appelle vecteur nul 0 (avec une fleche au dessus ) le vecteur AA=BB=...
Il n'a ni direction ni sens et sa norme vaut 0.
On appelle vecteur unitaire tout vecteur dont la norme vaut 1:
Si u est unitaire, alors ||u||=1

1.2 Opérations sur les vecteurs.

1) Addition/Soustraction.

Soient u et v deux vecteurs. (On reprend ici le système des flèches "sous-entendues" au dessus des noms des vecteurs, on ne parlera de toute façon de points que beaucoup plus loin).
On définit w = u+v à l'aide de la diagonale du parallèlogramme construit sur a et b.
On parle éventuellement de règle du parallèlogramme.

Il existe une seconde règle qui consiste à mettre u et v bout à bout pour obtenir w, c'est la règle du contour polygonal:

Propriétés de l'addition:

Soient a et b deux vecteurs:
--> a+b=b+a
--> (a+b) + c = a + (b+c)
--> a+0 = a
Il existe un unique vecteur X tel que:
a+X=0
Il s'agit de X= -a
Celui-ci s'observe aisément à l'aide de deux points A et B.
Soit AB un vecteur aussi noté a. Alors -a est le vecteur BA.
On a donc: -AB=BA

C'est cette définition du vecteur opposé qui permet de définir une soustraction.
Soient a et b deux vecteurs:

a - b = a + (-b)

RELATION DE CHASLES.

Une des plus importantes relations du calcul vectoriel.
Soient A et B deux points. Quel que soit M, on a:
AB= AM + MB
(vecteurs)